Boolean Arithmetic

Background

• LSB : least significants bit (최하위 비트)
• MSB : most significants bit (최상위 비트)

Binary Addition

컴퓨터에서 두 개의 n비트 2진수 덧셈을 구현하려면, 3개의 비트(한 쌍의 비트와 자리올림 비트)를 합산하는 논리 게이트를 구성하면 된다. 덧셈 후 자리올림 비트를 다음 자릿수로 보내는 것은, 3비트 가산 게이트의 배선을 적절하게 연결하면 간단하게 구현된다.

Signed Binary Numbers

n개의 숫자로 된 2진수로 표현 가능한 비트 패턴은 총 $2^n$ 개 이다. n 개의 숫자로 된 2진수 x가 있을 때, x 의 2의 보수는 다음과 같이 정의한다.

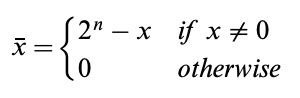
예를 들어, 5비트 2진수에서, -2 또는 음수 (00010) 를 나타내는 2의 보수는 2^5-(00010) = 32 - 2 = 30 = (11110) 이다.

2의 보수법을 n-bit 숫자에 적용하면, x+(-x) 는 늘 $2^n$ 이 된다. (즉, 1 다음에 n 개의 0이 온다.)

• 이 방식으로 총 $2^n$ 개의 부호있는 숫자를 표현할 수 있으며, 최댓값 및 최솟값은 각각 $2^{n-1}-1$ 과 $-2^{n-1}$ 이다.
• 모든 양수코드는 0으로 시작한다.
• 모든 음수 코드는 1로 시작한다.
• x 코드에서 -x 코드를 구하려면, x의 모든 비트를 뒤집고 1을 더하면 된다.

간단한 비트 단위 덧셈용 하드웨어만 있으면 2의 보수법을 이용해 어떤 부호 있는 두 개의 숫자라도 더할 수 있다. 뺄셈은 어떻게 할까? 뺄셈은 간단히 x-y=x+(-y) 를 계산하면 된고, 이렇게 하면 하드웨어 구현이 간단해 진다.

이 이론적 결과는 중요한데, 기본적으로 Arithmetic Logical Unit(ALU) 칩 하나에 모든 기초 산술과 논리 연산자를 담을 수 있다는 뜻이기 때문이다.

Specification

Half-Adder (반가산기)

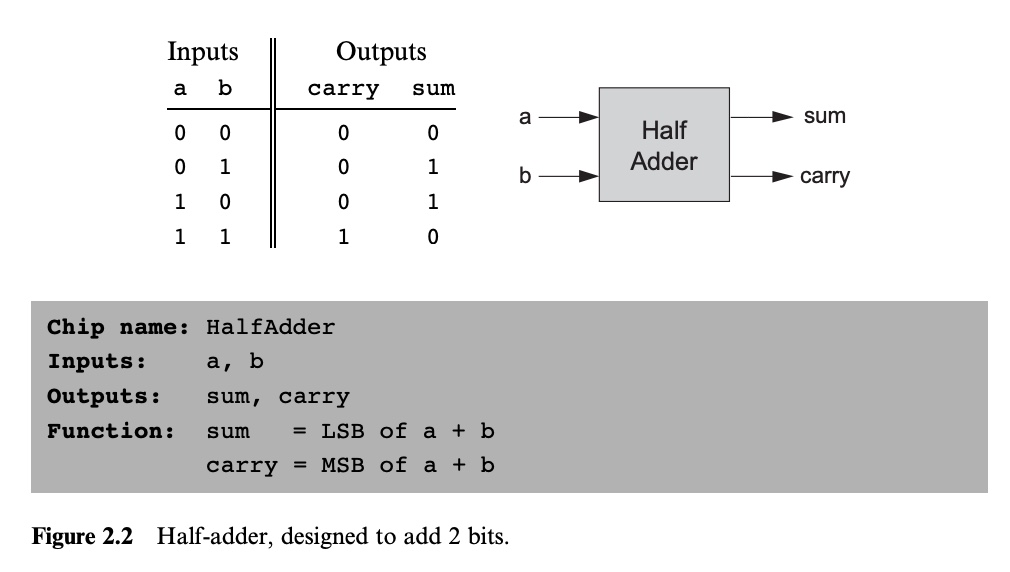
// Implementation
CHIP HalfAdder {
    IN a, b;    // 1-bit inputs
    OUT sum,    // Right bit of a + b
        carry;  // Left bit of a + b

    PARTS:
    Xor(a=a, b=b, out=sum);
    And(a=a, b=b, out=carry);
}

Full-Adder (전가산기)

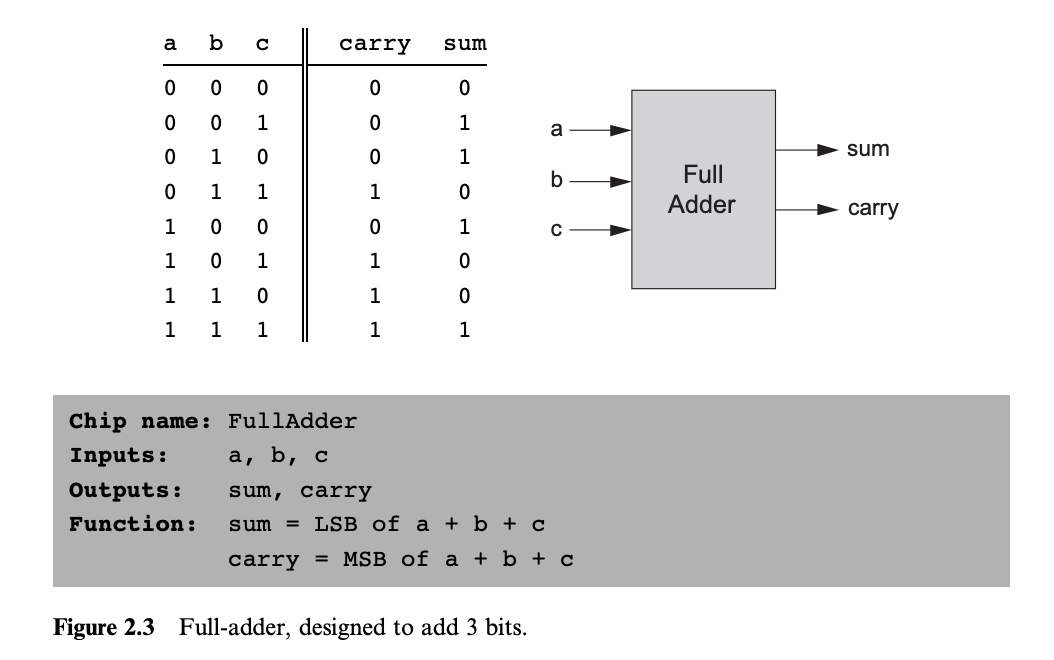
// Implementation
CHIP FullAdder {
    IN a, b, c;  // 1-bit inputs
    OUT sum,     // Right bit of a + b + c
        carry;   // Left bit of a + b + c

    PARTS:
    HalfAdder(a=a, b=b, sum=s1, carry=c1);
    HalfAdder(a=s1, b=c, sum=sum, carry=c2);
    Xor(a=c1, b=c2, out=carry);
}

Adder (가산기)

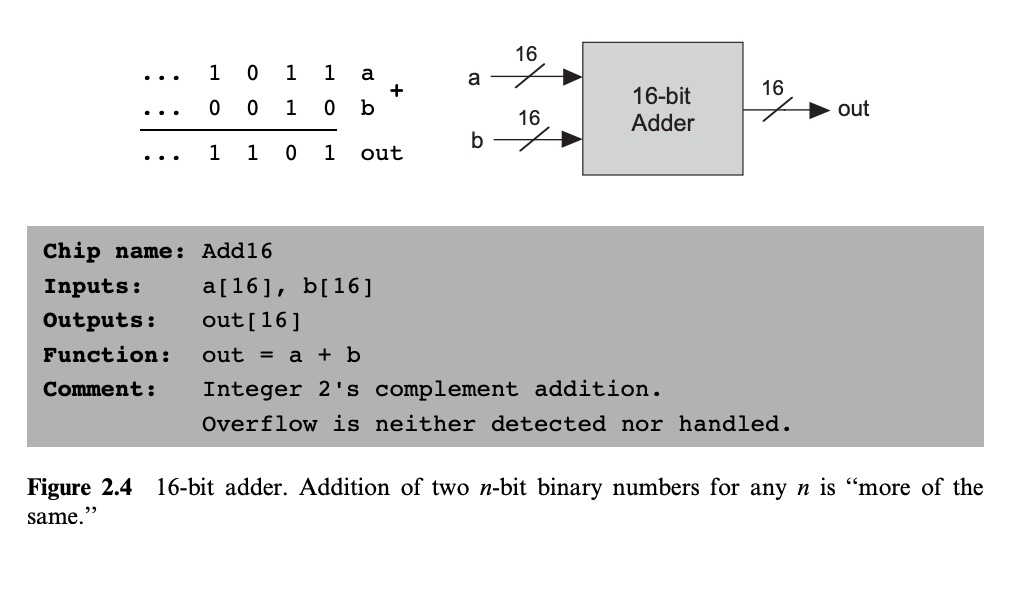
// Implementation
CHIP Add16 {
    IN a[16], b[16];
    OUT out[16];

    PARTS:
    HalfAdder(a=a[0], b=b[0], sum=out[0], carry=c0);
    FullAdder(a=a[1], b=b[1], c=c0, sum=out[1], carry=c1);
    FullAdder(a=a[2], b=b[2], c=c1, sum=out[2], carry=c2);
    FullAdder(a=a[3], b=b[3], c=c2, sum=out[3], carry=c3);
    FullAdder(a=a[4], b=b[4], c=c3, sum=out[4], carry=c4);
    FullAdder(a=a[5], b=b[5], c=c4, sum=out[5], carry=c5);
    FullAdder(a=a[6], b=b[6], c=c5, sum=out[6], carry=c6);
    FullAdder(a=a[7], b=b[7], c=c6, sum=out[7], carry=c7);
    FullAdder(a=a[8], b=b[8], c=c7, sum=out[8], carry=c8);
    FullAdder(a=a[9], b=b[9], c=c8, sum=out[9], carry=c9);
    FullAdder(a=a[10], b=b[10], c=c9, sum=out[10], carry=c10);
    FullAdder(a=a[11], b=b[11], c=c10, sum=out[11], carry=c11);
    FullAdder(a=a[12], b=b[12], c=c11, sum=out[12], carry=c12);
    FullAdder(a=a[13], b=b[13], c=c12, sum=out[13], carry=c13);
    FullAdder(a=a[14], b=b[14], c=c13, sum=out[14], carry=c14);
    FullAdder(a=a[15], b=b[15], c=c14, sum=out[15], carry=c15);
}

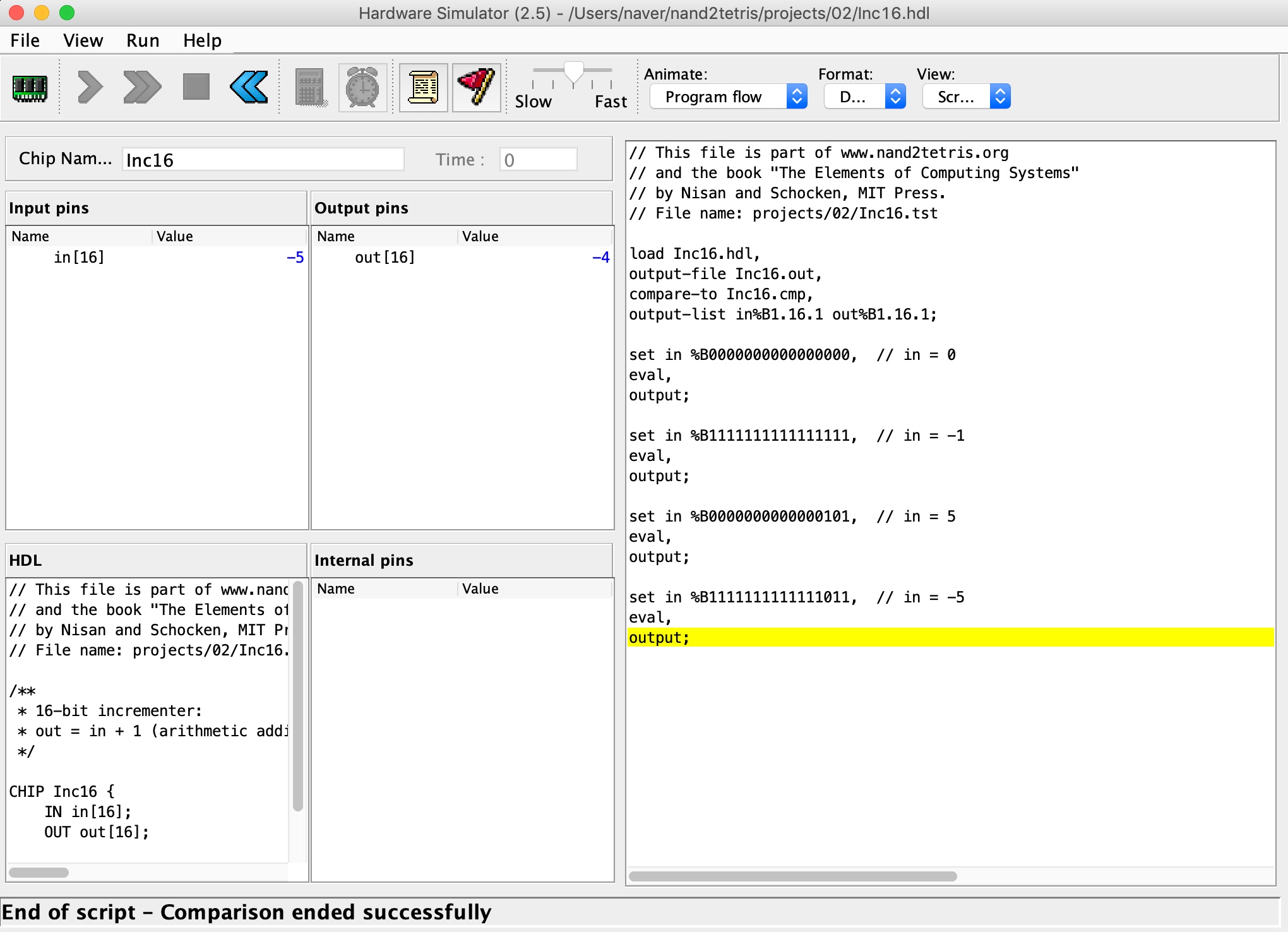
Incrementer (증분기)

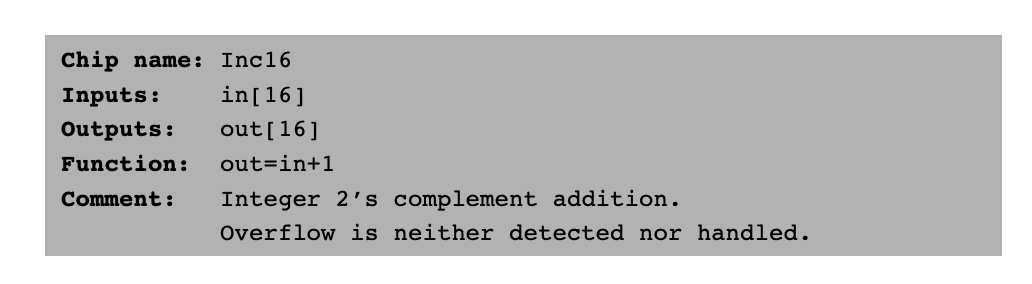
// Implemetation
CHIP Inc16 {
    IN in[16];
    OUT out[16];

    PARTS:
    Add16(a[0..15]=in[0..15], b[0]=true, b[1..15]=false, out[0..15]=out[0..15]);
}

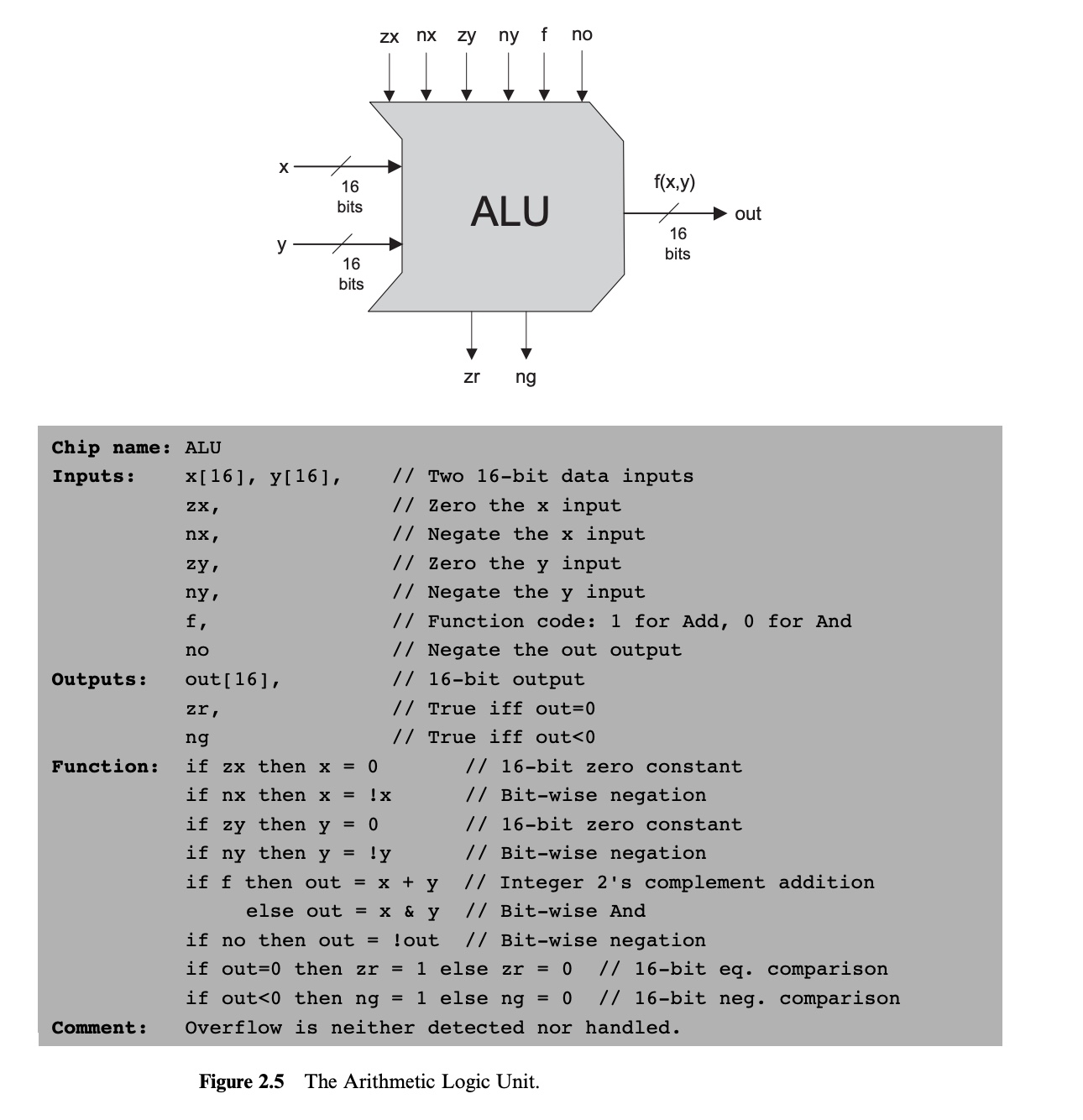
The Arithmetic Logical Unit (ALU)