Boolean Logic (불 논리)-1
Boolean Algebra (불 대수)
Boolean Algebra 는 true/false, 1/0, 예/아니오, on/off 같은 bool 값 (2진수) 를 다루는 대수학이다.

Boolean Expression (불 표현식)
불 함수는 진리표 말고도 입력값에 대한 불 연산으로도 표현이 가능하다.
위의 Figure 1.1 에 정의된 함수는 $f(x,y,z) = (x+y) * \neg z$ 라는 불 표현식과 같다.
예를 들어, 입력값 x=0, y=1, z=0 에 대해 이 표현식을 계산해보면,
y 는 1이므로 x+y=1 이고, $1 * \neg 0 = 1*1 = 1$ 이 된다.
8개의 가능한 입력값 조합에 대해 표현식을 다 계산해보면 표의 맨 오른쪽 열에 해당하는 값을 얻을 수 있으므로,
표현식과 진리표가 동등한 표현임을 알 수 있다.
Cononical Representation (정준 표현)
알고 보면 모든 Boolean Function 은 Cononical Representation (정준 표현) 이라고 불리는 불 표현식으로 표현이 가능하다.
위 함수의 진리표에서 함수 값이 1인 행들을 살펴보자.
각 행의 입력값에 대해 literal 을 And 연산으로 묶어 하나의 항으로 구성할 수 있다.
예를 들어, 그림 1.1에서 함수 값이 1인 세 번째 행을 보자.
이 행의 변수는 x=0, y=1, z=0 이므로 $\neg xy\neg z$ 라는 항을 만들 수 있다.
같은 방식으로 5행과 7행은 각각 $x\neg y\neg z, xy\neg z$ 이다.
이제 함수 값이 1인 모든 행에 대해 이 항들을 모두 Or 연산으로 묶으면, 주어진 진리표와 동등한 Boolean Expression 을 얻게 된다.
따라서 Figure 1.1 의 불함수에 대한 정준 표현은 $f(x,y,z) = \neg xy\neg z+x\neg y\neg z+xy\neg z$ 이다.
Two-Input Boolean Functions (2-입력 불 함수)
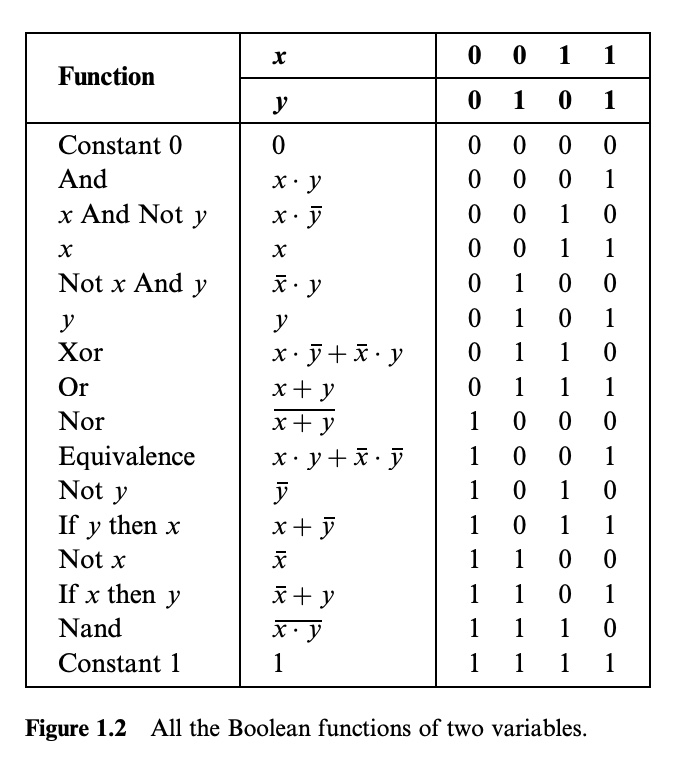
Figure 1.2 를 보면 n 개의 2진 변수에 대해 정의되는 불 함수의 수는 $2^{2^n}$ 개 임을 알 수 있다.
Equivalence: 두 변수의 진리값이 같을 때 결과값이 1인 등가함수이다. 즉, XOR의 반대.If-x-then-yor(x->y)or(x Implies y): x 가 0이거나 x,y 둘다 1일때 1을 반환하는 함수.If-y-tehn-x: y 가 0이거나, x,y 둘다 1일때 1을 반환하는 함수.
Nand 와 Nor 의 특징
and, or, not 연산을 이 함수로만 만들 수 있는 성질이 있다.
e.g) x or y = (x Nand x ) Nand (y Nand y)
그리고 모든 불 함수는 and, or, not 연산으로만 이루어진 정준 표현식으로 바꿔 쓸 수 있으므로, 결국 모든 불 함수는 Nand 연산만으로 표현할 수 있다.
즉, Nand 게이트만을 가지고 어떤 불 함수도 하드웨어로 구현 가능하다는 뜻이 된다.
HDL (Hardware Description Language)
오늘날 하드웨어 설계자들은 맨손으로 무엇인가를 만들어내는 대신, HDL(Hardware Description Language) 를 사용하여 칩 아키텍처를 설계하고 최적화 한다. 설계자는 칩 구조를 HDL 프로그램으로 작성하며, 이 프로그램은 가상의 컴퓨터 시뮬레이션을 통해 엄격한 테스트를 거치게 된다.
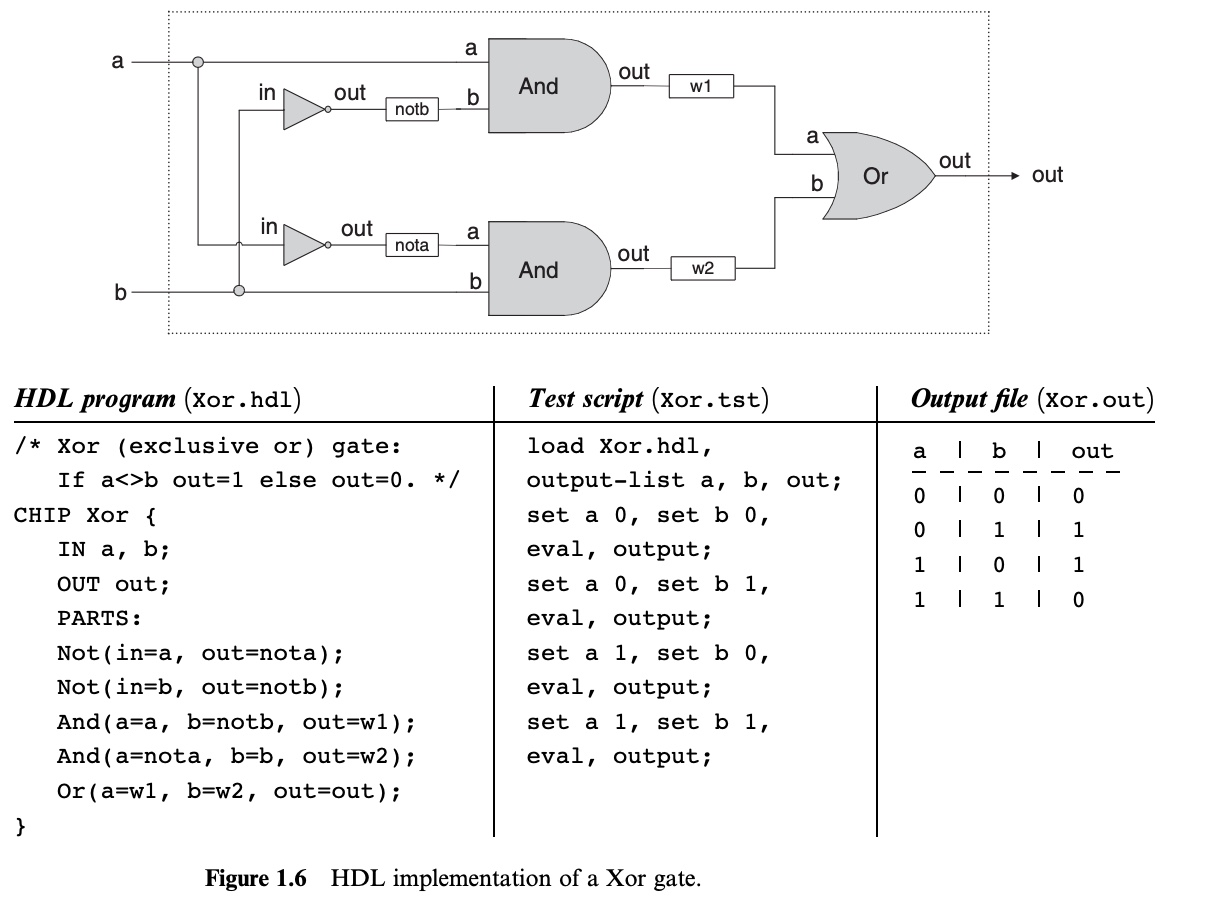
위 그림은 HDL 구현의 예시이다. 칩의 HDL 정의는 header 부분과 part 부분으로 나뉘는데, 먼저 header 는 칩 이름과 입력 및 출력 이름을 명시한다. 그리고 part 는 칩을 구성하는 아래 단계 파트들의 이름들과 연결 방식을 정의하게 된다.
Specification & Implementation
Nand Gate 만을 가지고 아래 Gate 들을 hdl 로 구현해보자. 각 게이트마다 명세와 내가 구현한 코드, 그리고 하드웨어 시뮬레이터로 검증한 결과 화면을 표시하였다.
Not Gate
// Specification
Chip name: Not
Inputs: in
Outputs: out
Function: If in=0 then out=1 else out=0.
// implementation
CHIP Not {
IN in;
OUT out;
PARTS:
Nand (a=in, b=in, out=out);
}
And Gate
// Specification
Chip name: And
Inputs: a, b
Outputs: out
Function: If a=b=1 then out=1 else out=0.
// implementation
CHIP Not {
IN in;
OUT out;
PARTS:
Nand (a=in, b=in, out=out);
}
Or Gate
// Specification
Chip name: Or
Inputs: a, b
Outputs: out
Function: If a=b=0 then out=0 else out=1.
// implementation
CHIP Or {
IN a, b;
OUT out;
PARTS:
Nand (a=a, b=b, out=nandout);
Nand (a=a, b=nandout, out=anand);
Nand (a=nandout, b=b, out=bnand);
Nand (a=anand, b=bnand, out=cnand);
Nand (a=cnand, b=cnand, out=dnand);
Nand (a=nandout, b=dnand, out=out);
}
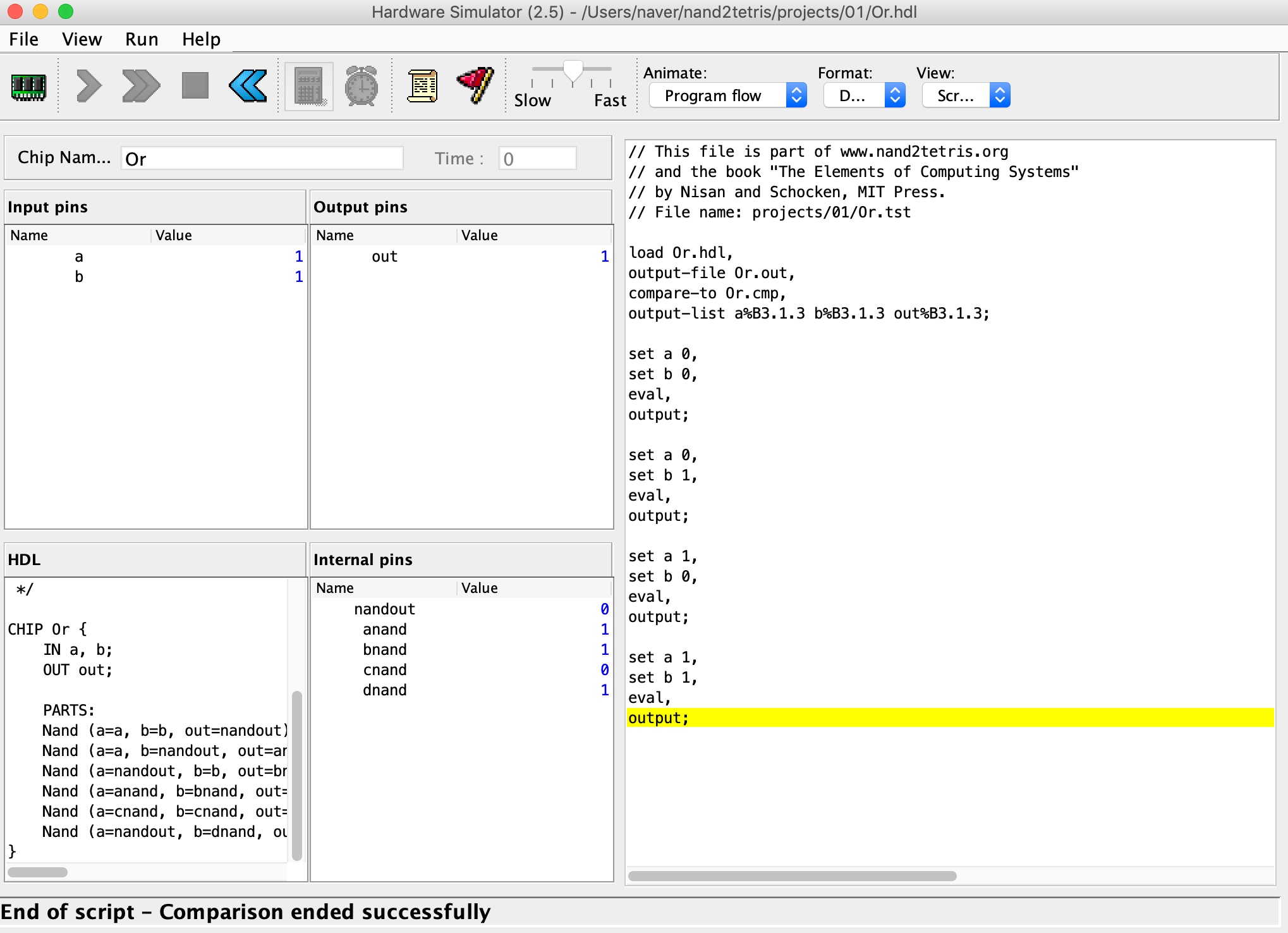
Xor Gate
// Specification
Chip name: Xor
Inputs: a, b
Outputs: out
Function: If a=/b then out=1 else out=0.
// implementation
CHIP Xor {
IN a, b;
OUT out;
PARTS:
Nand (a=a, b=b, out=nandout);
Nand (a=a, b=nandout, out=anand);
Nand (a=nandout, b=b, out=bnand);
Nand (a=anand, b=bnand, out=out);
}
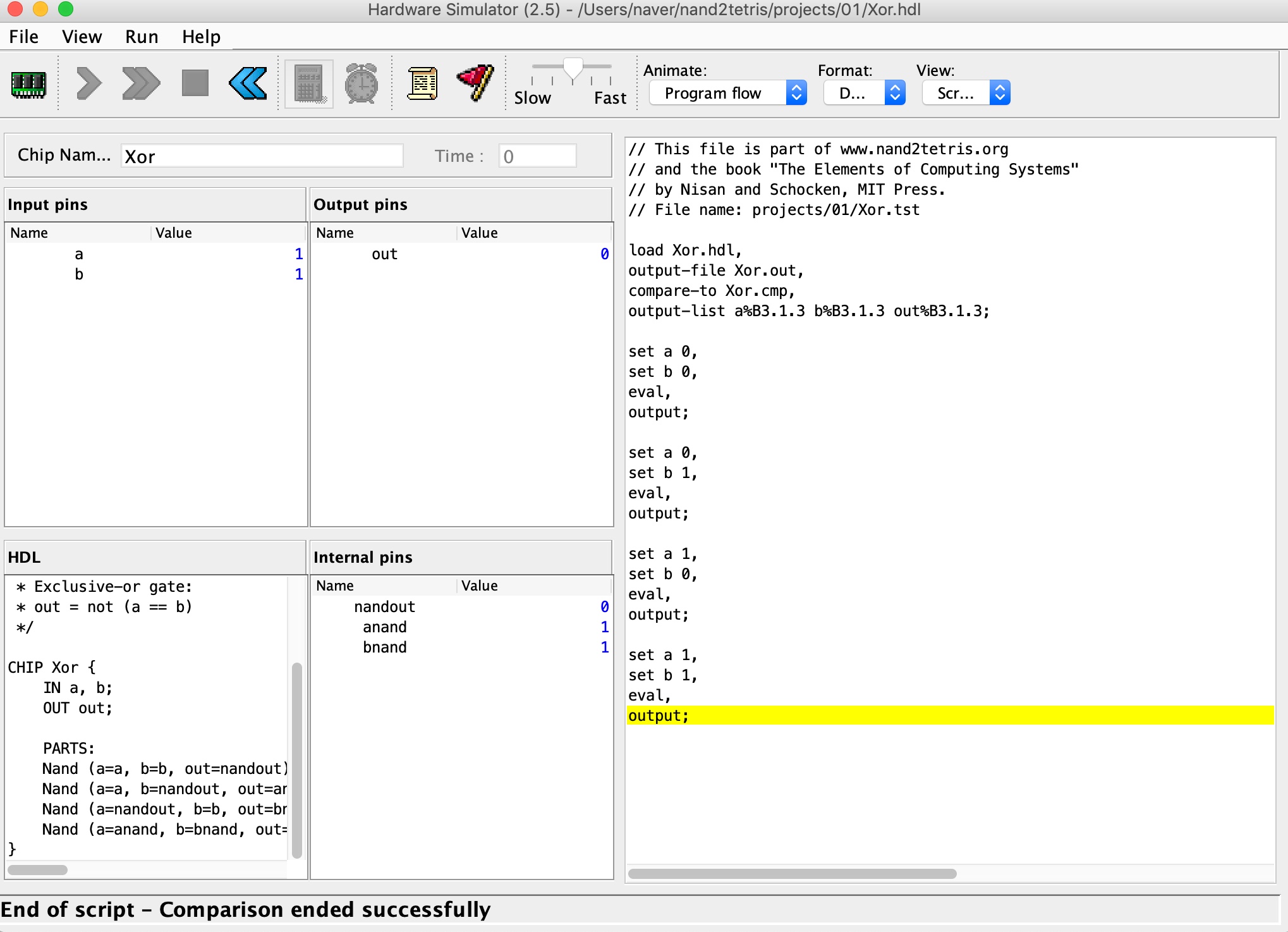
Multiplexor
// Specification
Chip name: Mux
Inputs: a, b, sel
Outputs: out
Function: If sel=0 then out=a else out=b.
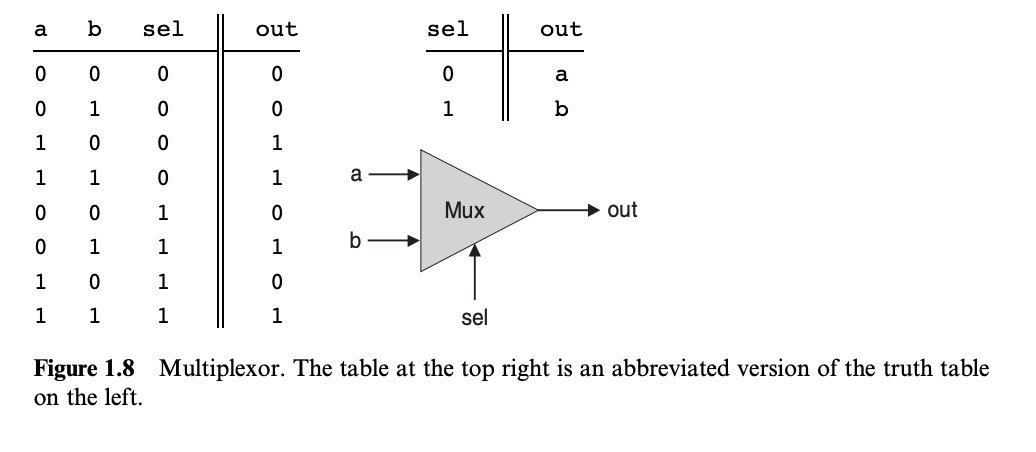
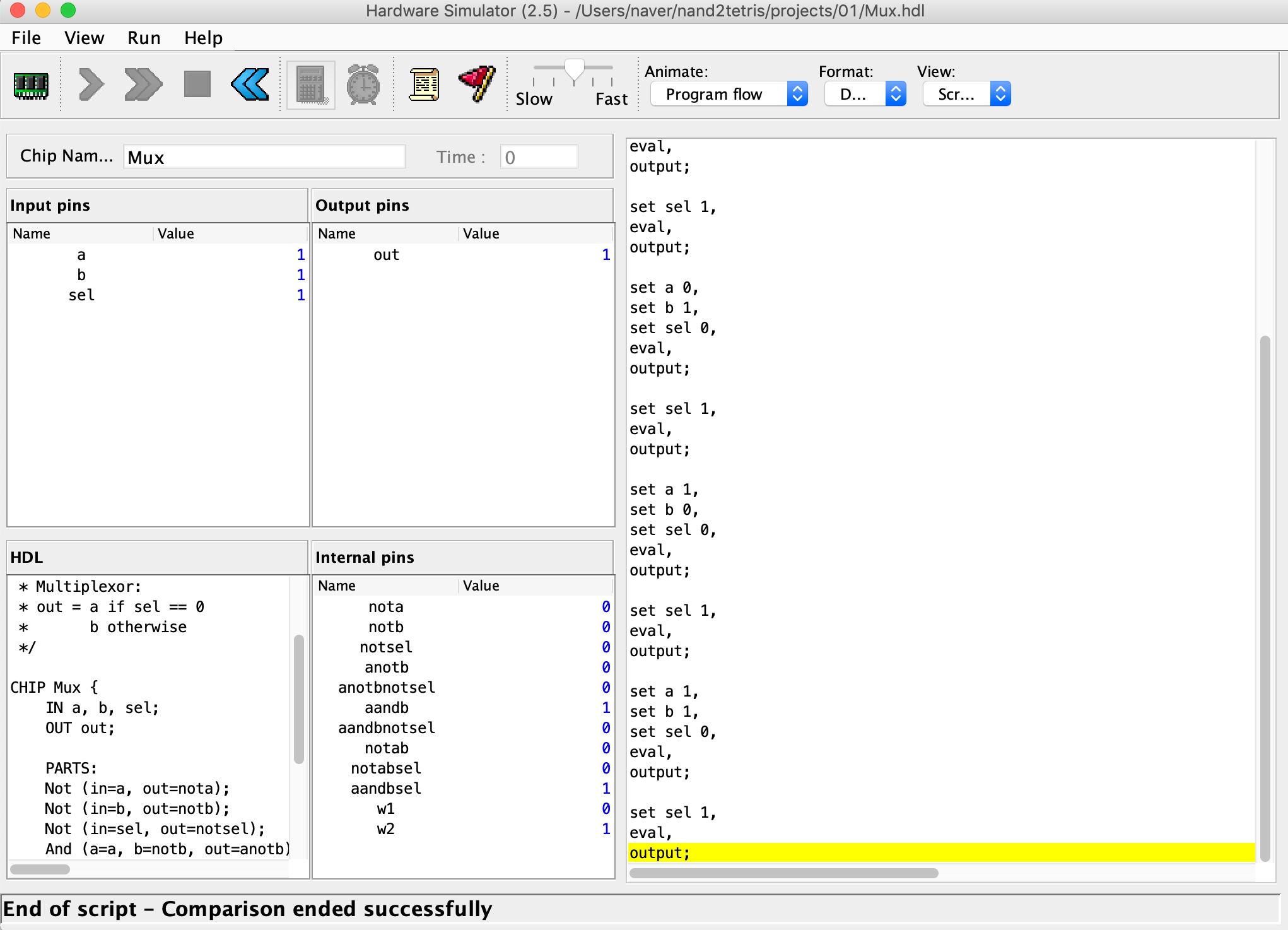
위 Multiplexor 의 정준 표현식은 $a\neg b\neg sel + ab\neg sel + \neg absel + absel$ 이 되므로 아래와 같이 구현할 수 있다.
CHIP Mux {
IN a, b, sel;
OUT out;
PARTS:
Not (in=a, out=nota);
Not (in=b, out=notb);
Not (in=sel, out=notsel);
And (a=a, b=notb, out=anotb);
And (a=anotb, b=notsel, out=anotbnotsel);
And (a=a, b=b, out=aandb);
And (a=aandb, b=notsel, out=aandbnotsel);
And (a=nota, b=b, out=notab);
And (a=notab, b=sel, out=notabsel);
And (a=aandb, b=sel, out=aandbsel);
Or (a=anotbnotsel, b=aandbnotsel, out=w1);
Or (a=notabsel, b=aandbsel, out=w2);
Or (a=w1, b=w2, out=out);
}
Demultiplexor
// Specification
Chip name: DMux
Inputs: in, sel
Outputs: a, b
Function: If sel=0 then {a=in, b=0} else {a=0, b=in}.
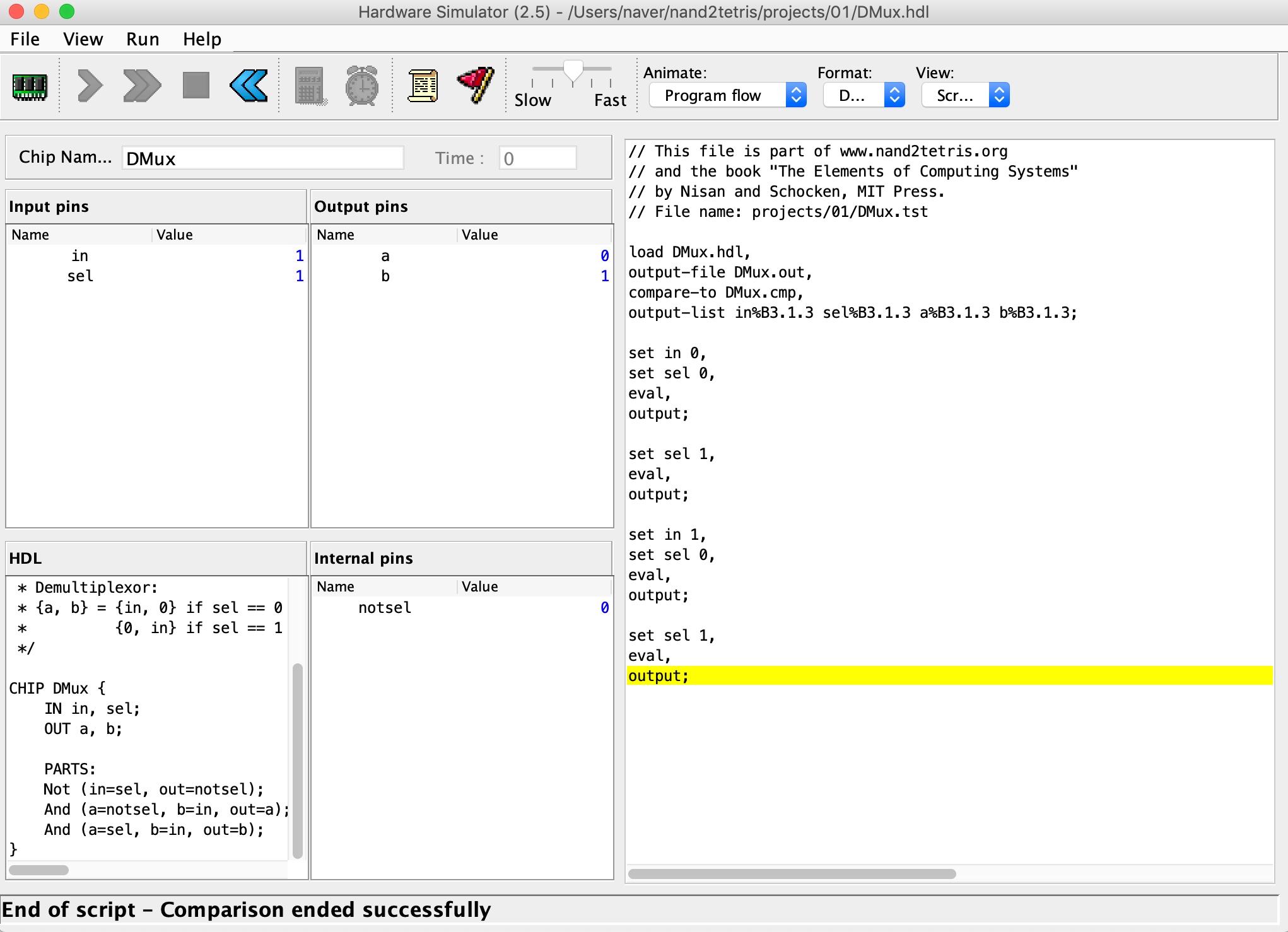
DMux 는 구현 방법이 잘 떠오르지 않아 DMultiplex Logic Diagram 을 찾아보았다. 다이어그램을 확인해보니 하나의 Not Gate 와 두개의 And Gate 로 연결해서 만들 수 있었다.
구현 로직은 아래와 같다.
CHIP DMux {
IN in, sel;
OUT a, b;
PARTS:
Not (in=sel, out=notsel);
And (a=notsel, b=in, out=a);
And (a=sel, b=in, out=b);
}
댓글남기기